Regression analysis
is defined as applying a set of statistical
processes to estimate the relationship between variables. Many
techniques are involved in modeling and analyzing these variables.
Regression analysis
helps us understand how the values of dependent
variables changes when there's a variation in
any of the independent variables while dealing with
multiple independent variables.
We can even
understand the variation trend of dependent variables by slightly varying any
one of the independent variables and keeping others fixed.
Let’s start with
Simple Linear Regression and proceed further with multiple linear regression.
Simple Linear Regression :
As mentioned before,
Simple Linear Regression is a process of regression in finding relationship of
dependent and independent continuous quantitative variables. It is called Simple because there's only one
independent / explanatory or predictor variable that is used to predict the
relationship dependency
In
"Multiple" Linear regression, two or more independent variables are
used to predict the dependency of a Response variable.
Simple Linear
Regression is represented by the formula Y = β0
+ β1* X + Ɛ
Here, β1 is the independent ( explanatory )
variable and Y is the dependent variable. That means, the slight variation of
independent variable ( β1 ) will result in variation of predictor ( β0 ) variable.
Identifying /
estimating the Correlation & Co-variance between these two variables by
regression is defined as the relationship between these two variables.
Covariance shows the direction of the relationship
between these variables
Correlation shows the strength of the relationship
between these variables.
Covariance, as name
suggests, shows how the dependent variable varies when the independent variable
is varied.
Let us consider an
equation y = mx + c
y = mx + c is an equation of a straight line
and the direction of variation on y can
be measured by the variation that happens on x.
Lets consider a
sample data set of temperature in Fahrenheit v/s heartbeat. ( for the sake of simplicity, I have considered only
male data to ignore gender column from the dataset )
|
degrees
|
beats per minute
|
|
98.4
|
84
|
|
98.4
|
82
|
|
98
|
78
|
|
97.9
|
72
|
|
98.5
|
68
|
|
98
|
67
|
|
97.4
|
78
|
|
98.8
|
78
|
|
99.5
|
75
|
|
97.1
|
75
|
|
98
|
71
|
|
98.9
|
80
|
|
99
|
75
|
|
98.6
|
77
|
|
96.7
|
71
|
Data Sourced from http://www.statpoint.net/OpenSample.aspx
Now, here Y = beats per minute & X = temperature.
To understand the
covariance, let's take the mean of X & Y
Sample mean of Y Ymean = 98.2 degrees. With the formula provided here
Sample mean of X Xmean = 75.4 degrees.
Understanding the
deviation of each observation from the mean Yi & Xi and taking the product.
Product = ( Yi -
Ymean ) * ( Xi - Xmean )
|
Quadrant
|
Yi - Ymean
|
Xi - Xmean
|
( Yi - Ymean ) (
Xi - Xmean )
|
Relationship
|
|
1
|
+
|
+
|
+
|
+
|
|
2
|
+
|
-
|
-
|
-
|
|
3
|
-
|
+
|
-
|
-
|
|
4
|
-
|
-
|
+
|
+
|
Plotting the graph
with X & Y coordinates and understanding the linear relationship between X
& Y as follows :
If the plotted
points are in 1st and 3rd Quadrant ->
relationship is positive, i.e., if X
increases, Y also increases
If the plotted
points are in 2nd and 4th Quadrant -> relationship is negative, i.e., if X
increases, Y decreases.
Hence, covariance of
the variables can be defined as :-
Understanding the
covariance between Y & X will provide the direction of how the variables
are related to each other.
Substituting the
values of the above table in Covariance formula :
COV(Y, X) = ((98.4 -
98.21)(84-75.4)+(98.4-98.21)(82-75.4)+98 - 98.21)(78-75.4)+……)/ ( 15 - 1))
COV(Y, X) = 13.42000 / 14
COV(Y, X) = 0.9585 * 100 = 95.85%
If Cov(Y,X) > 0
then we can understand that Y & X are positively correlated if Cov(Y,X)
< 0 then Y & X have negative relationship.
With this, we can
understand that the direction for Y & X is positive
Understanding the
Covariance, we can derive the Correlation
of the variables :-
Correlation can be
defined as :
Where Sy & Sx are the standard deviations of Y
& X respectively.
Substituting the
Covariance and Standard Deviation :-
COR(Y, X) = 0.9585 / ( 0.75 * 12.10)
COR(Y, X) = 0.1059 * 100 = 10.59 %
This indicates the
strength of variables - for every unit increase in X there will be a 10.59%
increase in Y.
Standardizing the Data
Standardizing the
data means, If the data of Y & X are ranging between thousands of units and
they can't be compared or plotted in a graph, these numbers will be
standardized based on certain rules.
- Subtract the observations from mean value.
- Divide each observation by standard deviation ( check here for standard deviation )
Standardizing Y
& X, we will arrive at the above mentioned formula for Correlation.
Correlation can be defined as Covariance between the
standardized variables or the ratio of the Covariance to the standard deviation
of the two variables.
Calculating the
Correlation, result lies between -1 & +1
-1 <= COR ( Y,X ) <= +1
Hence, these
properties make the correlation of Y & X ( Response & Independent
variables ) a useful quantity for measuring the direction
and strength of the relationship between variables.
More the Cor(Y,X)
towards +1, relationship between Y & X is said to be stronger and vice
versa.
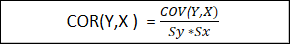
No comments:
Post a Comment