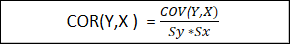Multiple Linear
Regression is a process that uses multiple explanatory variables to predict the outcome of a response variable. The purpose of Multiple Linear Regression is to
model the linear relationship between multiple variables and the response
variable.
This is also an
extension of Linear Regression that involves more than one independent variables.
The Formula for Multiple Linear Regression is : Yi = β0 + β1x1 +
β2x2 + … + βnxn + ϵ
Multiple linear
regression model with n independent
variables and one dependent variable Y.
Here
Yi <- the dependent variable and
X1, X2, X3 ….., Xn <- independent variables
/ model parameters / explanatory variables
β0 <-
is a constant or Intercept of the slope and
ϵ = the error ( residuals )
As explained
earlier, multiple regression model extends to several explanatory variables. A
simple linear regression is used to make predictions about one variable based
on the information that is known about another variable. here.
However, multiple Linear Regression model is extended to predict using the information that is known about multiple
variables.
The basic purpose
of the least-square regression is to fit a hyper-plane into ( n+1 ) dimension that
minimizes the SSE.
SSE <- Sum of
Squares of Residual errors ( SSE ) ∑( Yi − Yihat ) ^2 where Yihat is the
predicted value
SSR <- is the
Sum of Squares due to Regression ∑( Yihat − Yiµ ) ^2 where Yiµ is the mean value of data
SST <- Total Sum of Squared deviations in Yi from its mean Yihat
SST = SSR + SSE
R-Squared : The coefficient of determination (
R-Squared ) is a square of the correlation co-efficient between dependent
variable Y and the fitted values Yhat
Correlation coefficient between response variable
& Predictor variables
Generally, R-Squared = SSR / SST . Substituting the above formula for SSR = SST - SSE
R-Squared Formula
becomes 1
- SSE / SST
Taking an example
of 50-startups data. We will be
predicting the profit of the companies located in different locations.
We will also see
which variable is highly correlated with the response variable.
Steps to predict
using Multiple Linear regression
- After importing the datafile
- Validate the data, look at the categorical variable
- apply OneHotEncoding feature to categorical variables. I will explain how this works in a separate blog.
- Split the dataset into Train and Test set
- Fit the model using Multiple Linear Regression
Here, using all
the variables to fit the model might not give a good accuracy, because, there
could be some variables that are not significant or correlated with the
response variable and hence might not add a lot of value in the prediction.
Hence, there are
multiple different approaches to find the highly correlated variables that
contribute for building an appropriate model.
- Use All - Use all the variables to predict the response variable, eliminate them based on the significance P-Value
- Stepwise Regression -
- Backward Elimination : Below steps are followed to build a model using Backward Elimination process
- Select Significant level ( P- Value ) - ( 0.5 - 5 ) %
- Fit the model
- Remove variables that higher than P-Value ( least significant one by one )
- Fit the model
- Continue the process until you find all the variables that are highly correlated with Response variable
- Forward Selection :
- Select Significant level ( P- Value ) - ( 0.5 - 5 ) %
- Fit the model with first variable
- Remove / include the variables that less than P-Value ( highly significant variables one by one)
- Fit the model
- Continue the process until you find all the variables that are highly correlated with Response variable
- Score Comparison - Compare the scores of P-Values for eliminating the variables one by one.
- Select Goodness of Fit ( Akaike Information Criteria ) : StepAIC method to find the right set of variables that are highly significant for building a model.
You can find the
code at GitHub
Looking at the code in R :-
# Multiple Linear Regression
# Created by Deepak Pradeep Kumar
#Setting working directory
setwd("<<Set
Your Folder here>>")
# Importing the dataset
dataset =
read.csv("50_Startups.csv")
#Encoding the Categorical variable
dataset$State =
factor(dataset$State,
levels = c('New
York','California','Florida'),
labels = c(1,2,3))
# Splitting the dataset into
trainingset and testset
library(caTools)
set.seed(101)
split =
sample.split(dataset$Profit, SplitRatio = 0.8)
trainingset =
subset(dataset, split == TRUE)
testset =
subset(dataset, split == FALSE)
# Feature Scaling is not needed as
it will take care of Fit function that we use.
# Fitting Multiple Linear
Regression to training set
regressor =
lm(formula = Profit ~ R.D.Spend + Administration + Marketing.Spend + State,
data = trainingset)
summary(regressor)
#Removing Administration and
Fitting the model
regressor1 =
lm(formula = Profit ~ R.D.Spend +
Marketing.Spend + State,
data = trainingset)
summary(regressor1)
#Removing State and Fitting the
model
#Ideally, we add Administration
back and remove only state and fit the model. In this case, it is fine to
remove both the variables
regressor2 =
lm(formula = Profit ~ R.D.Spend + Marketing.Spend,
data = trainingset)
summary(regressor2)
#Removing Marketing Spend and also
and Fitting the model
regressor3 =
lm(formula = Profit ~ R.D.Spend,
data = trainingset)
summary(regressor3)
# Backward Elimination using
StepAIC method
# Use this method immediately
after Fitting the model
#install.packages('MASS')
library(MASS)
stepAIC(regressor)
# Predicting the TEST SET Results
y_predictor =
predict(regressor, newdata = testset)
|